




With regard to energy demand in transport one has to differentiate between primary and secondary energy demand.
When comparing different means of traffic used to transport passengers, it is not the energy demand in absolute terms of a vehicle which is important but the energy demand of a given amount of traffic (specific energy demand). It is therefore useful to calculate the energy demand on the basis of the unit person-kilometre (pnkm), as it is usually done. 1 pnkm is equal to a route of 1 km length, covered by one person.
The specific secondary energy demand is derived from:
Average fuel consumption of a car in long-distance traffic is 9.1 liters/100 km.* Since this figure for 1992 remained constant during the past 20 years, it cannot be expected to change essentially until 2010 *. This is true at least for the high economic growth scenario assumed in this study: Technological progress in car and motor construction will be compensated by the trend to bigger and more comfortable cars.
On average, a car in long-distance traffic is occupied with 1.7 persons*.
In long-distance traffic by bus the following two types of vehicles are predominantly used:
In charter bus traffic the degrees of capacity utilization of the buses are with 80 % even slightly higher than in regular bus traffic.
One can assume that there won't be any fundamental changes in bus transport by the year 2010, neither with regard to capacity utilization nor with regard to fuel consumption.
Therefore, fuel demand per person in bus transport is as follows:
Bus
Between Hamburg and Berlin, Lufthansa uses almost exclusively planes of the type Fokker 50. These 50-seat turboprop planes consume*:
with a capacity utilization of 100 %: 4.9 liters/100km
with a capacity utilization of 70 %: 5.3 liters/100 km
with a capacity utilization of 50 %: 6.0 liters/100 km
Possibly, a slightly lower value of consumption can be set for the year 2010; however, since air traffic is already playing a small role in quantitative terms and both scenarios of this study even assume the end of air traffic we do not have to investigate this question any further.
With the factor 0.7, the degree of capacity utilization
between Hamburg and Berlin is estimated to be more or less equal to the average
of the total Lufthansa fleet: Though it is true that the internal German air traffic
with conventional jets has a degree of capacity utilization of
0.5 to 0.6, the comparably small turboprop airplanes however, can create a
more demand-oriented supply than the significantly larger airplanes.
Specific secondary energy demand for the railway is measured in Wh/pnkm (Watt-hours per person-kilometre) measured at the overhead contact wire. Since energy demand varies strongly, depending on the route, we have done computer simulations for the existing rail connections Hamburg-Büchen-Wittenberge-Berlin and Hamburg-Uelzen-Stendal-Berlin.
The result of the simulation is an energy demand of 25 Wh/pnkm for the route via Wittenberge and an IC-train with ten carriages (590 seats), and an electric locomotive of the type 120 (with a maximum speed of 160 km/h).
For the future ICE-connection the following options are possible:
With regard to the route we have assumed an extended and newly-built route Hamburg-Uelzen-Stendal-Berlin, with the following estimated maximum speeds per section:
Energy demand of the ICE for the extended and newly-built route Hamburg-Uelzen-Stendal-Berlin
| energy demand at the overhead contact wire in Wh/Pnkm | ||
| 250 km/h | 300 km/h | |
| ICE 3, 8 carriages,
low number of seats per coach | 42,3 | 46,5 |
| ICE 3, 14 carriages, high number of seats per coach | 30,6 | 42,3 |
Average degree of capacity utilization in German rail passenger transport is 50 %*. To attain the specific secondary energy demand, the listed figures have to multiplied by the factor 2.
According to the tasks of this study we have to presume an optimised ICE-connection
with 250 km/h maximum speed. This means, that the above mentioned consumption
figure for the 14-carriage -ICE, related to the assumed speed, is used for our
calculations.
Specific energy demand of the Transrapid:
4 sections, 430 km/h: 95 Wh/pnkm
5 sections, 430 km/h: 88 Wh/pnkm
6 sections, 430 km/h: 83 Wh/pnkm
These figures are related to exit of the transformer station. The losses in the undercarriage, which is part of the engine, have been included in this calculation. The result coincides with the data of the regional traffic development plan which was made for the Transrapid route, consisting of 6-section vehicles*.
Higher vehicle length figures lead to better energy demand results per seat, for both the railway and the Transrapid. The reason for this is the fact that only the first coach has to displace the air (front side resistance). All the following coaches are in the slipstream of the first one.
The prediction of approximately 15 million passengers per year as presumed in the regional traffic development plan is too high, even when assuming an economic growth of 90 % between 1988 and 2010.* One has to correct this value rather by 1/3 downwards which is equal to 11.1 million passengers/year*. Due to this lower passenger figure it seems to be appropriate to have only 5-section-trains running every 15 minutes, rather than the planned 6-section trains every 12-15 minutes*. This is why we have assumed the utilization of the slightly more energy-intensive 5-section-trains. Would the traffic predictions be adapted to the real economic development - which is not the task of this study - then only 4-section-trains would be utilised. These require even more energy per seat.
With regard to the degree of capacity utilization for the Transrapid, we can take the corresponding average figure for long-distance trains of the DB AG which is 50 %.
By introducing variable ticket pricing*, both railway and Transrapid can achieve
a degree of capacity utilization between 0.7 and 0.75.
However, neither the Deutsche Bahn AG nor the Transrapid are definitely planning
such pricing models.
To make the fuel consumption of the car, bus and airplane with the electricity demand of railway and Transrapid comparable, one has to convert the calorific values of fuel per liter into the electrical value kilowatt hour. The conversion figures are:*
1 l diesel = 9.8 kWh
1 l petrol = 9.0 kWh
1 l kerosene = 9.6 kWh.
The weighted average figure for the conversion of the calorific value of the car fuels diesel and petrol is 9.1 kWh.
The following figures have been calculated for the secondary energy demand of the various long-distance vehicles used to transport passengers between Hamburg and Berlin:
Overall view of the fuel and electricity demand (secondary energy) in long-distance passenger transport Hamburg - Berlin
| fuel in l/100 km | energy in Wh/pkm | |
| car with an average of 1.7 persons | 5,35 | 487 |
| single-decker, 80 % capacity utilization | 0,71 | 70 |
| airplane Fokker 50, 70 % capacity utilization | 5,30 | 512 |
| IC
with 10 carriages, max. speed 160 km/h | 50 | |
| ICE 3 with 14 carriages, max. speed 250 km/h | 61,2 | |
| Transrapid
5 sections max. 430 km/h | 176 |
With regard to efficiencies one has to consider transport losses on the one hand, and losses when refining crude oil, respectively in the power station when generating electricity.
The efficiencies for the various processes are:
(1) 92.5 % for the refinery of crude oil into kerosene, diesel and petrol*
(2) 98.5 % for the distribution of diesel and petrol at petrol stations*
(3) 99.5 % for the distribution of fuels in large amounts to airports and power stations*
(4) 36.5 % for power stations used in electricity generation for the railway in 1992*
(5) 46.5 % for power stations used in electricity generation for the railway in 2010 (see below)
(6) 92.6% for the distribution in the railway electricity grid, including the transformer station of the railway*
(7) approximately 95 % for the distribution in the electricity grid for Transrapid power, excluding the transformer station
(8) approximately 90 % in the transformer station of the Transrapid.
Older sources have indicated an efficiency of 86 % in the transformer station of the Transrapid.*; In this study it is assumed that this lower degree of efficiency can be improved up to 90 %.
The above mentioned efficiencies will not have changed essentially by the year 2010, except for the efficiency of thermal power stations. For these plants, remarkable technological progress has been achieved during the past few years. A continuation of this development will lead to a higher efficiency in 2010.* Therefore, this kind of technological progress will reduce primary energy demand for the railway and the Transrapid. While in 1950, the efficiency of a thermal power station (without combined heat and power) was only 18 %, in 1980 the most modern installations had already an efficiency of 37 % which is equal to the average of all thermal power stations in 1992. The most modern power stations today arrive at an efficiency of up to 58 % (gas-or oil-fired). The efficiency of power stations using coal is somewhat lower. Nevertheless, by 2010 an increased efficiency by 10 points, between 36.5% and 46.5%, seems to be realistic.
When looking at the whole efficiency chain one has to multiply the percentages with each other as factors 0.00 to 1.00. Thus, two efficiencies of 50 % (two times 0.50) result in a total efficiency of 25 % (factor 0.25).
With regard to the different vehicles used to transport passengers, the efficiency chains and total efficiencies are as follows (the figures given in brackets refer to the above explanation of efficiencies):
Total efficiency car, bus: 90.5
%
composed of:
(1) refinery 92.5 %
(2) distribution 98 %
Total efficiency airplane: 92 %
composed of:
(1) refinery 92.5 %
(3) distribution 99.5 %
Total efficiency railway 1992: 33.5 %
composed of:
(3) distribution to power stations 99.5 %
(4) power station 36.5 %
(6) distribution electricity grid 92.6 %
Total efficiency railway 2010: 43 %
composed of:
(3) distribution to power stations 99.5 %
(5) power station 46.5 %
(6) distribution electricity grid 92.6 %
Total efficiency Transrapid 1992: 31 %
composed of:
(3) distribution to power stations 99.5 %
(4) power station 36.5 %
(7) distribution electricity grid 95 %
(8) transformer stations 90 %
Total efficiency Transrapid 2010: 39.5 %
composed of:
(3) distribution to power stations 99.5 %
(5) power station 46.5 %
(7) distribution electricity grid 95 %
(8) transformer stations 90 %
The fact that - when operating the Transrapid - the energy demand is subject to extreme fluctuations remained unconsidered in this calculation. These fluctuations of the energy demand occur only in a very weakened form for a - fictional - ICE traffic which would use the same route as the Transrapid. When power stations have to deal with such extreme load fluctuations, their efficiency tends to be lower than with a relatively constant load which is required for the operation of a railway.
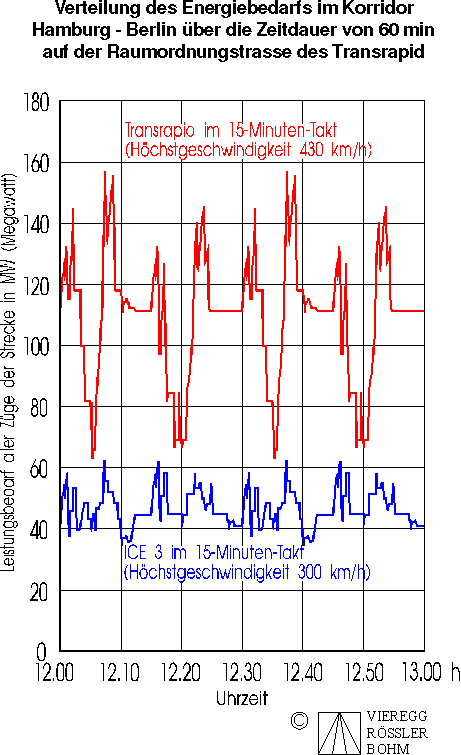
Distribution of the energy demand in the corridor Hamburg - Berlin over a time span of 60 min on the planned route of the Transrapid, both trains in 15 min intervals with the same capacity

Based on the above derived figures for secondary energy and efficiency we come to the following primary energy demand:
Primary energy demand per vehicle used to transport passengers in the corridor Hamburg - Berlin
| secondary energy Wh/pnkm | total efficiency Wh/pnkm | primary energy Wh/pkm | |
| car with 1.7 person | 487 | 90.5 % | 538 |
| bus single-decker | 70 | 90.5 % | 77 |
| airplane Fokker 50, 70 % capacity utilization | 512 | 92.0 % | 557 |
| IC with 10 carriages, max. speed 160 km/h* | |||
| - with power station technology 1992 | 50 | 33.5 % | 149 |
| - with power station technology 2010 | 50 | 43.0 % | 116 |
| ICE 3 with 14 carriages, max. speed 250 km/h* | |||
| - with power station technology 1992 | 61 | 33.5 % | 182 |
| - with power station technology 2010 | 61 | 43.0 % | 142 |
| Transrapid 5 sections, max. speed 430 km/h* | |||
| - with power station technology 1992 | 176 | 31.0 % | 568 |
| - with power station technology 2010 | 176 | 39.5 % | 446 |
| * 50 % capacity utilisation |
The high energy demand of the Transrapid, compared to the high-speed railway transport, is surprising. A considerable share of the extra energy demand can be put down to the higher speed, since energy demand increases with velocity squared.
But even at the same speed the energy demand for the Transrapid is significantly higher than the one for a comparable wheel-rail-technology:
Energy demand of Transrapid and ICE at a constant speed
of 300 km/h,
capacity utilization 50 %
| secondary | total | primary | |
| energy | efficiency | energy | |
| Wh/pnkm | Wh/pnkm | ||
| Transrapid with 5 sections | 103 | 39.5 % | 260 |
| ICE 3 with 14 carriages and | 72 | 43 % | 167 |
| a high seating capacity |
The extra energy demand of the Transrapid is remarkable. It can be put down to several differences between the two vehicles used to transport passengers which are inherent in the system:
This contradiction should be resolved, when making oneself aware of the following facts: